Complexidade de Algoritmo e Notação Big-O
Olá Viajante, seja bem vindo. Hoje vamos falar de um dos assuntos que mais assombram iniciantes no mundo da engenharia de software: Complexidade de Algoritmos e Notação O-Grande (Big-O Notation). Normalmente esses caras vem na garupa de outros assuntos ainda mais escabrosos, como Algoritmos e Estruturas de Dados. Mas calma lá, vamos por partes.
Meu objetivo aqui é dar uma introdução leve sobre o assunto, abordando de forma pragmática para quem está iniciando na carreira e talvez, assim como eu, não tem fortes bases teóricas em matemática.
Usarei alguns exemplos implementados em Python. Acredito que mesmo que você não tenha familiaridade com a linguagem, o código será de fácil entendimento, mas tentarei sempre explicar o que cada snippet faz. Vamos lá.
Complexidade de Algoritmos
A complexidade de um algoritmo é uma análise que prevê como o código se comportará com entradas maiores de dados. Nessa análise, não serão consideradas variáveis como hardware, rede, I/O ou latência, que podem impactar a execução positiva ou negativamente, apenas a quantidade de instruções executadas pelo código.
Isso é importante porque não queremos medir se o código roda em X segundos ou com Y gigas de memória.
Imagine um mundo hipotético onde não precisamos aguardar ciclos do processador, escalonamento de processos, alocação de memória, interpretação da linguagem ou qualquer outra variável externa ao nosso código.
A complexidade é quanto tempo ou recursos adicionais serão necessários para processar entradas maiores para o mesmo código.
Tempo e Espaço
Normalmente são feitas duas analises de complexidade distintas para cada algoritmo: tempo de execução e espaço de memória.
Com o resultado dessas analises, você será capaz de decidir se o algoritmo encaixa nas restrições do seu ambiente, negócio, hardware, etc ou se é necessário abrir mão da eficiência em alguma delas.
Complexidade de Tempo
Complexidade de tempo é a ordem de grandeza de quanto tempo seu código levará para executar dada uma entrada maior.
Existem casos onde independente do tamanho da entrada, o resultado é computado sempre dentro do mesmo tempo. Exemplo:
def nome_completo(nome: str, sobrenome: str) -> str:
return f'{nome} {sobrenome}'
Não importa o tamanho das strings nome e sobrenome, o resultado sempre é calculado como o mesmo número de instruções. Nesse caso são 3: criação da string literal; interpolação das variáveis; retorno da função.
Chamamos esse tipo de complexidade de constante. Pode se dizer que o algoritmo da função nome_completo é constante em tempo de execução.
Já em outros casos, a quantidade de elementos na entrada pode afetar diretamente o número de instruções que temos que calcular. Exemplo:
def contar_caracteres(texto: str) -> dict:
resultado = {}
for letra in texto:
resultado[letra] = resultado.get(letra, 0) + 1
return resultado
Nesse caso, as instruções: atribuição à variável letra, atribuição ao dicionário, procura de chave no dicionário e soma, serão feitas um número de vezes determinado pelo tamanho da string de entrada. Ou seja, cada letra adicional na string aumenta em 4 o número total de instruções a processar.
Chamamos esse tipo de complexidade de linear. Pode se dizer que o algoritmo da função contar_caracteres é linear em tempo de execução.
Podemos ver que mesmo ambas as funções recebendo strings como entrada, a primeira executa seu algoritmo sempre no mesmo tempo (constante), enquanto a segunda aumenta seu tempo proporcionalmente ao tamanho da entrada (linear).
Complexidade de Espaço
Complexidade de espaço é a ordem de grandeza de quanto recusos (normalmente memória ram) serão utilizados dada uma entrada maior.
O princípio é o mesmo mas agora medimos uma coisa diferente: os recursos alocados pelo algoritmo para realizar a tarefa.
Utilizando os mesmos exemplos usados anteriormente:
def nome_completo(nome: str, sobrenome: str) -> str:
return f'{nome} {sobrenome}'
def contar_caracteres(texto: str) -> dict:
resultado = {}
for letra in texto:
resultado[letra] = resultado.get(letra, 0) + 1
return resultado
A função nome_completo cria uma nova string, composta das duas strings anteriores com um espaço de separação. Isso quer dizer que ao passo que as strings nome e sobrenome crescem, a memória necessária para alocar a string que será retornada também aumenta, fazendo da função nome_completo um algoritmo linear em espaço de memória.
Já na função contar_caracteres temos uma análise interessante. Dependendo da entrada ela pode ser constante ou linear.
Imagine que se tivermos o valor de texto com apenas uma letra ou apenas letras iguais, o dicionário resultante será sempre de tamanho fixo (1 chave string e 1 valor inteiro), fazendo dele um algoritmo constante em memória.
No entanto, caso tenhamos uma string com todas as letras diferentes, o dicionário resultante terá N pares de chave string e valor inteiro, sendo N o tamanho da string de entrada, fazendo dele um algoritmo linear em memória.
Essas diferenças dependentes de caso são comuns de serem encontradas e é um ótimo gancho para destrincharmos esse assunto. Bora!
Análise de Melhor e Pior Caso
Como vimos no algoritmo de contar caracteres, a análise de complexidade pode variar dependendo de casos específicos. Por isso, é sempre importante deixar claro de qual caso (melhor, pior ou médio) estamos calculando a complexidade.
def contar_caracteres(texto: str) -> dict:
resultado = {}
for letra in texto:
resultado[letra] = resultado.get(letra, 0) + 1
return resultado
No nosso algoritmo de contar caracteres, o melhor caso seria uma entrada em que não precisamos entrar no loop ou adicionar algo ao dicionário, ou seja, uma entrada vazia. Nesse caso teríamos uma complexidade constante em espaço (apenas a criação de um dicionário vazio) e ignoraríamos as instruções dentro do loop for, sendo constante em tempo. Da mesma forma, o pior caso seria uma entrada com todos os caracteres diferentes. Deixando o tamanho do dicionário igual ao da string (linear em memória) e sempre precisamos passar por todos os caracteres da string, sendo linear em tempo.
Ao criar nossas notações normalmente vamos falar apenas do pior caso. No entanto, avaliar esses casos é importante para sabermos qual deles está mais próximo do contexto onde o algoritmo será aplicado. Por exemplo, se esse algoritmo fosse implementado para contar nomes de pessoas brasileiras, raramente teríamos os melhores casos e os piores casos. O caso típico seria strings com apenas alguma dezenas de caracteres, com poucos caracteres diferentes. Da mesma forma, se fosse aplicado a livros de qualquer idioma, as strings seriam consideravelmente maiores com a quantidade de caracteres possíveis muito maior.
A análise de caso típico também é importante para criar otimizações. Otimizações são maneiras mais eficientes de executar uma subtarefa específica do problema. Um exemplo interessante é o da função builtin len da linguagem python. Sendo a função len normalmente utilizada para contar o tamanho de objetos primitivos (listas, dicionários, strings), existe uma otimização para que a execução desse algoritmo seja feita em tempo constante. Caso o objeto não seja primitivo, é delegada a tarefa de calcular o tamanho do objeto para o método padrão __len__, que pode ser implementado pelo desenvolvedor.
Notação Big O
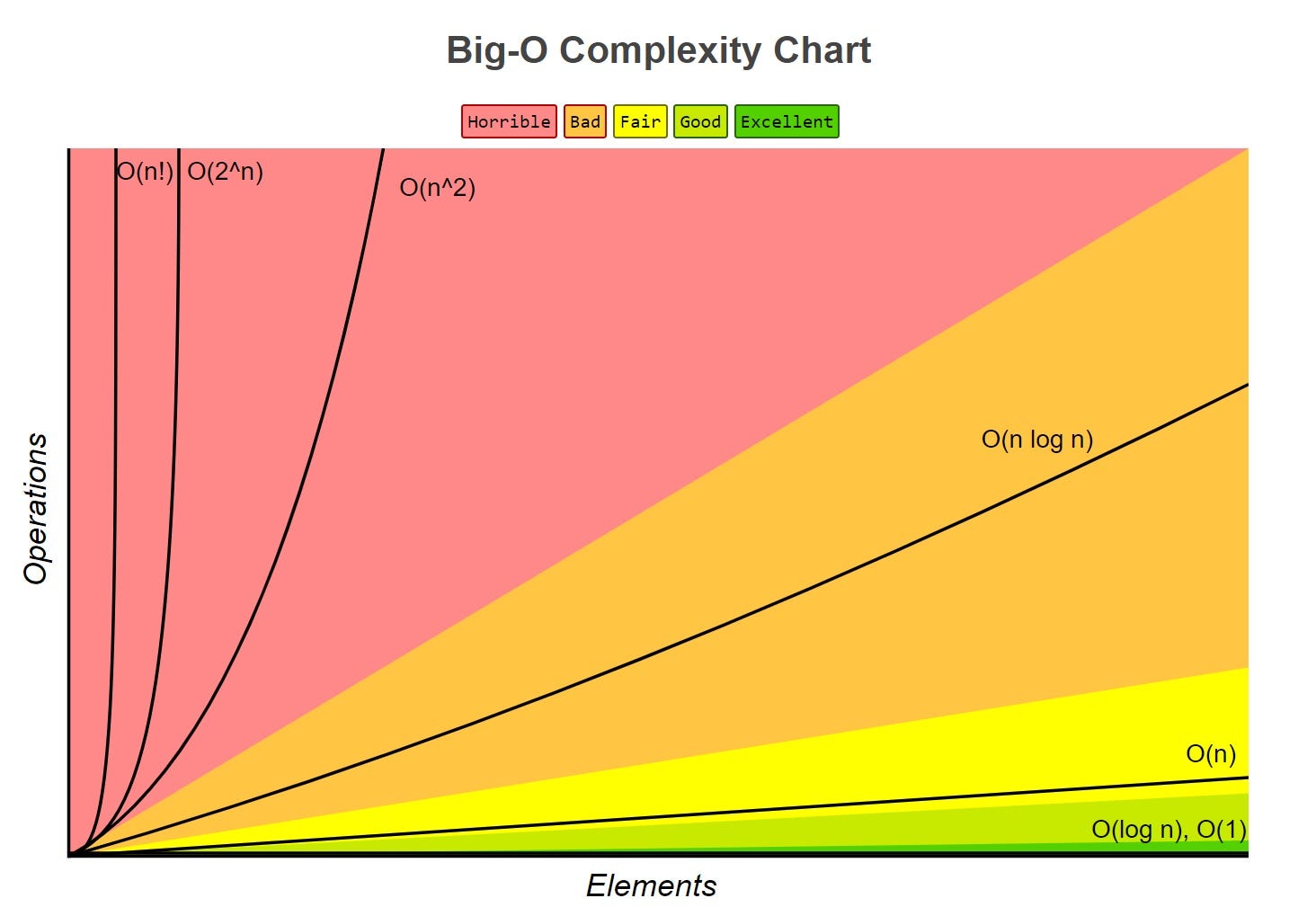
Sabendo o que é complexidade de algoritmo, fica fácil entender Notação Big-O. Já sabemos que nosso algoritmo pode variar em tempo de execução ou consumo de recursos dependendo do tamanho da entrada. Notação Big-O, é apenas uma forma matemática para determinar quanto ele de fato cresce.
A Notação Big-O é definida pela letra O que representa Ordem ou a taxa de crescimento de uma função, seguida por uma expressão que pode ou não envolver incógnita para referenciar tamanhos variáveis das entradas. Como exemplo, vamos analisar a complexidade do algoritmo abaixo:
def maior(lista: list[int]) -> int:
'''Encontra o maior número de uma lista.'''
maior_numero = None # (1)
for item in lista: # (2)
if maior_numero is None or item > maior_numero: # (3)
maior_numero = item # (4)
return maior_numero
Para determinar a complexidade de tempo, a primeira coisa a se fazer é contar as operações linha a linha do nosso algoritmo e verificar quais podem se repetir dependendo da entrada:
(1) Uma atribuição, que é feita em tempo constante, temos 1 operação.
(2) Logo abaixo temos um for loop, que faz a atribuição de uma variável para cada item da lista. Nesse caso temos uma valor que pode variar, então daremos o nome de N ao tamanho da lista, temos 1 + N operações.
(3) As operações de comparação serão feitas também para todos os itens da lista, temos 1 + N + N ou 1 + 2N.
(4) A atribuição da variável dentro do if será feito pelo menos uma vez e no máximo N vezes. Vamos assumir o pior caso e dizer que será feita todas as vezes, temos 1 + 2N + N ou 1 + 3N.
Aqui temos a quantidade aproximada de instruções feitas por nosso algoritmo no pior caso. No entanto, normalmente desconsideramos as constantes e coeficientes da expressão, pois ao passo que N fica cada vez maior, esses ficam cada vez mais irrelevantes. Dessa forma, reduzimos nossa expressão para N. E com isso temos chegamos a notação O(N).
Um algoritmo O(N) também é chamado de Algoritmo Linear. Podemos dizer que a função maior é linear em tempo, o que quer dizer que o tempo de processamento da função cresce de maneira proporcional ao tamanho da entrada. Se passarmos um valor de N 10 vezes maior, o algoritmo levará aproximadamente 10 vezes mais tempo para terminar.
Fazendo o mesmo exercício para a análise de espaço em memória temos:
def maior(lista: list[int]) -> int:
'''Encontra o maior número de uma lista.'''
maior_numero = None # (1)
for item in lista: # (2)
if maior_numero is None or item > maior_numero:
maior_numero = item
return maior_numero
(1) Uma variável para armazenar o maior número e (2) uma variável que será reatribuída para armazenar o item da iteração. Então temos 2.
Nas analises de espaço não consideramos a entrada como parte do custo. Por isso não computamos o tamanho da lista em nossa expressão, continuamos com a ordem de 2.
Como não podemos simplesmente desconsiderar a constante, por que não teríamos expressão alguma como resultado, a notação usada é O(1).
O(1) é também chamado de Algoritmo Constante. Podemos dizer que a função maior é constante em espaço.
O que objetivamente estamos dizendo é que N não faz parte da ordem de grandeza, ou seja, não importa o quanto N cresça a resposta da função será executada sempre com o mesmo custo de memória.
Normalmente esse entendimento é confuso para quem é novo no assunto. Uma confusão comum é achar que o valor a colocar na expressão depende do tipo de objeto (e.g. um int gasta menos memória que um long, por exemplo) então deveriamos ter algo como 2N nesse caso. Mas não funciona assim. Lembre-se que estamos interessados na ordem (taxa de crescimento) da função e não no detalhe de implementação.
O tal do Log
Ainda falaremos de algoritmos com ordem de grandeza bem piores que o linear, no entanto, entre um algoritmo constante e um linear existe uma diferença gigantesca. Nesse espaço existe a complexidade logarítmica, que escala pior que o constante mas ainda bem melhor que o linear. Vários algoritmos famosos na computação caem no caso de complexidade logaritmica. Como exemplo, vamos analisar o código abaixo:
def busca_binaria(lista, valor):
indice_inicial = 0
indice_final = len(lista)
while indice_inicial <= indice_final:
meio = indice_inicial + int((indice_final - indice_inicial)/2)
if lista[meio] == valor:
return meio
elif lista[meio] < valor:
indice_inicial = meio
else:
indice_final = meio
return -1
Nessa implementação do algoritmo de busca binária retornamos o índice do valor caso ele exista na lista, caso contrário retornamos -1. Esse é um algoritmo muito famoso por ser bastante simples e eficiente. A cada iteração, o algoritmo de busca binária divide a entrada ao meio e escolhe a parte onde o possível resultado está até chegar na posição do valor ou em uma lista vazia. O único tradeoff, é que para realizar a busca binária, você precisa que a lista de entrada esteja ordenada.
No quesito complexidade, vemos que o algoritmo depende do tamanho da lista, mas ele faz um número de operações muito menor que seu tamanho, pois a cada etapa ele divide o problema ao meio. O pulo do gato para essa análise é entender que “dividir o problema ao meio” é a representação de uma proporção logaritmica, nesse caso, de base 2.
Isso acontece por que a logaritmação é um dos inversos da exponenciação. Ou seja, ao contrário de uma potência de base 2 onde para cada incremento de 1 ao expoente nosso resultado dobra (e.g. 2^2=4 e 2^3=8). Para uma logaritmação de base 2, para cada vez que o logaritmando dobrar, o resultado será incrementado em 1 (e.g. log2(4)=2 e log2(8)=3).
No nosso caso, a base de divisão é 2 e o logatimando é o tamanho variável do parâmetro “lista”, que chamaremos de N em nossa notação. Então temos O(log N) para a busca binária, complexidade logarítmica em tempo.
Para espaço você provavelmente já sabe a resposta: Visto que guardamos apenas 3 variáveis de inteiros temos complexidade constante, O(1).
As aparências enganam
Cuidado com a tentativa excessiva de reduzir linhas de código. Como já dizia o poeta “Nem tudo que brilha é relíquia, nem joia”, existem casos onde algoritmos “menores” operam em complexidades muito piores.
Voltando ao nosso exemplo de algoritmo para encontrar o maior numero de uma lista não ordenada:
def maior(lista: list[int]) -> int:
maior_numero = None
for item in lista:
if maior_numero is None or item > maior_numero:
maior_numero = item
return maior_numero
Vamos dizer que refatoramos o código para resolver o mesmo problema em apenas duas linhas. Como abaixo:
def maior(lista: list[int]) -> int:
lista.sort()
return lista[-1]
O problema implícito nesse código é que ordenar uma lista é uma tarefa muito mais complexa (pun intended) do que apenas iterar nos elementos dela, sendo de complexidade O(N log N) no caso médio, para alguns algoritmos até O(N^2) no pior caso. Isso quer dizer que a para cada item em N será executado um subtarefa de complexidade O(log N). Mesmo a linguagem Python implementando um ótimo algoritmo de ordenação, que no melhor caso pode ser O(N) em tempo, ainda é O(N log N) nos casos médio e pior.
Ou seja, adicionando a linha lista.sort() nós pioramos nossa complexidade de O(N) para O(N log N), também chamado de Algoritmo Linearitmico (na real ninguém chama disso não, é ene-lógue-ene mesmo). Por isso é importante não só saber analisar a complexidade do seu algoritmo, mas qual a complexidade das operações implementadas pela linguagem ou framework que esteja utilizando. Ao adicionar uma linha de código de complexidade O(N log N) nosso algoritmo inteiro passa a ter essa complexidade.
Ao infinito e além
Uma complexidade acima de O(N log N) já é considerada bem ruim. No entanto, existem algoritmos com complexidades ainda piores. Os mais conhecidos sendo:
- Complexidade O(N^2), quadrática, onde para cada item da entrada você executará N operações, sendo N o tamanho da entrada. Por exemplo o caso de for loops aninhados, como no algoritmo de ordenação Bubble Sort:
def bubble_sort(lista):
for i in range(len(lista) - 1):
for j in range(i + 1, len(lista)):
if lista[j] < lista[i]:
lista[j], lista[i] = lista[i], lista[j]
return lista
- Complexidade O(2^N), exponencial, onde a cada novo item adicionado a entrada, o número de instruções dobra. Por exemplo, o caso de implementação ingênua de uma sequencia de fibonacci recursiva.
def fib_recursive(n):
if n == 1 or n == 2:
return 1
return fib_recursive(n-1) + fib_recursive(n-2)
No entanto, pensar apenas na complexidade sem levar em concideração o contexto da sua aplicação pode levar a otimizações prematuras e as vezes a um desempenho até pior.
Como Rob Pike explica no tópico 3, de suas 5 regras da programação quando o valor de N for pequeno (spoiler: normalmente N será pequeno), algorítmos refinados são mais lentos. Isso acontece por que suas constantes são muito grandes (lembram aquelas que desconsiderarmos na análise final?).

Qual é o N da questão ?
Nem sempre é tão simples encontrar o valor de N (o tamanho total da sua entrada), ou até podem existir outras variáveis que impactam o tempo ou espaço do seu algoritmo.
Voltando a um exemplo conhecido:
def nome_completo(nome: str, sobrenome: str) -> str:
return f'{nome} {sobrenome}'
Como o valor de ambas as entradas (nome e sobrenome) são interpolados na string retornada, a representação de N nesse algoritmo não está ligada apenas uma das entrada e sim as duas juntas.
Imagine que a função receba como entrada um nome e sobrenome de 5 e 10 caracteres respectivamente, a função criará em memória uma string de 16 caracteres. Já ao passar um nome de 10 caracteres e um sobrenome de 5 caracteres, a função criará da mesma forma uma string de 16 caracteres.
Para sermos explicitos na demonstração desse fator, poderíamos descrever a complexidade de espaço da função nome_completo como O(N + M) onde N = nome e M = sobrenome, por exemplo. Isso facilita o entendimento e deixa explicito que ambas as entradas interferem na complexidade de espaço do algoritmo.
Amortização
Durante a análise podemos esbarrar em casos de algoritmos que de vez em quando rodam numa complexidade diferente das demais. Como por exemplo a inserção de elementos no fim de um array dinâmico.
As inserções ao fim de um array dinâmico são O(1) em tempo, no entanto, após um certo número o array interno enche e é necessário fazer a cópia de todo o array para um novo, essa operação custará O(N) em tempo. Isso sugere que temos um algoritmo O(N) em pior caso. No entanto, como essas operações acontecem poucas vezes, sua relevância diminui ao longo que o algoritmo é executado mais vezes.
Para representar a complexidade aproximada para esses casos definimos um Pior Caso Amortizado, que na operação de inserção em um array dinâmico, seria O(1). Imagine que ao rodarmos o algoritmo alguns milhões de vezes, teremos uma tendência tão proxima a O(1), que as operações feitas em tempo O(N) não são relevantes.
Finalmentes
Se você é iniciante e chegou até aqui, parabéns.
Esse assunto é complexo e pode ser sufocante para quem está começando. Se foi isso que você sentiu, eu recomendo colocar esse assunto numa lista de estudos e voltar nele algumas vezes ao longo da sua jornada.
Até logo.
Agradecimentos
Revisão por Emily Faccin
Recomendações
Ned Batchelder - Big-O: How Code Slows as Data Grows - PyCon 2018
Comments